目录
快速导航-

课程教材教法 | 核心素养视角下高中数学教材习题与课程标准的一致性研究
课程教材教法 | 核心素养视角下高中数学教材习题与课程标准的一致性研究
-

课程教材教法 | 深度学习视域下数学变式教学的高阶设计
课程教材教法 | 深度学习视域下数学变式教学的高阶设计
-

课程教材教法 | 高中数学不同版本教材数列概念内容的比较研究
课程教材教法 | 高中数学不同版本教材数列概念内容的比较研究
-
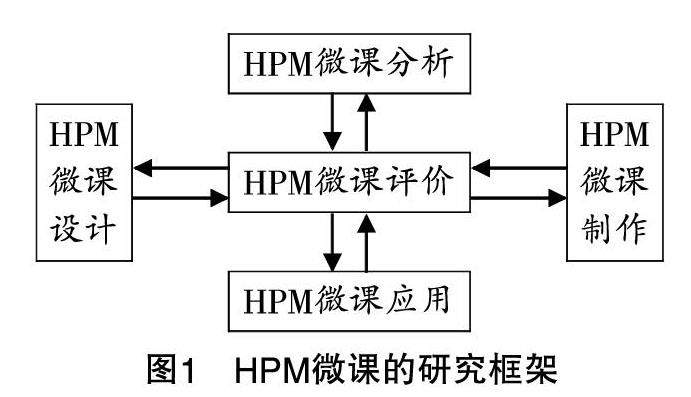
教学实践 | HPM微课在高中数学教学中的应用研究
教学实践 | HPM微课在高中数学教学中的应用研究
-

教学实践 | 方法承载思维 提炼启迪智慧反思提高素养
教学实践 | 方法承载思维 提炼启迪智慧反思提高素养
-

教学实践 | 通过创造性使用教材助力日常教学
教学实践 | 通过创造性使用教材助力日常教学
-

教学实践 | 经历知识生成 发展核心素养
教学实践 | 经历知识生成 发展核心素养
-

教学实践 | 结构性问题下借助数学实验的概念教学设计
教学实践 | 结构性问题下借助数学实验的概念教学设计
-

教学实践 | 探究式教学在高三一轮复习教学中的应用研究
教学实践 | 探究式教学在高三一轮复习教学中的应用研究
-
教学实践 | 基于个性化学习的高中数学“思考力课堂”构建与实施研究
教学实践 | 基于个性化学习的高中数学“思考力课堂”构建与实施研究
-

教学实践 | 单元大概念视域下高中数学学习中创新思维能力的养成研究
教学实践 | 单元大概念视域下高中数学学习中创新思维能力的养成研究
-

教学实践 | 巧用问题驱动 发展探究能力
教学实践 | 巧用问题驱动 发展探究能力
-

教学实践 | 系统设计问题 问道单元教学
教学实践 | 系统设计问题 问道单元教学
-
教学实践 | 刍议深度学习视域下概念教学有效提问的措施
教学实践 | 刍议深度学习视域下概念教学有效提问的措施
-

教学实践 | APOS理论模式与应用策略的研究
教学实践 | APOS理论模式与应用策略的研究
-
教研在线 | 指向逻辑推理素养涵育的高中数学教学实践研究
教研在线 | 指向逻辑推理素养涵育的高中数学教学实践研究
-
教研在线 | 核心素养导向下的高中数学高效课堂建构策略研究
教研在线 | 核心素养导向下的高中数学高效课堂建构策略研究
-
教研在线 | 高中数学课堂的多元化教学评价模式实践探究
教研在线 | 高中数学课堂的多元化教学评价模式实践探究
-
教研在线 | 基于深度学习的高中新教材概念教学实践研究
教研在线 | 基于深度学习的高中新教材概念教学实践研究
-

问题探索 | 跨章节一题多解,实现知识互联
问题探索 | 跨章节一题多解,实现知识互联
-

问题探索 | 构建思维框架 超越题型教学
问题探索 | 构建思维框架 超越题型教学
-
教学反思 | 对培养高中生数学阅读能力的几点建议
教学反思 | 对培养高中生数学阅读能力的几点建议
-

教学反思 | 对讲评课的一些认识与思考
教学反思 | 对讲评课的一些认识与思考
-

教学技巧 | 动态生成,让高中数学课堂焕发光彩
教学技巧 | 动态生成,让高中数学课堂焕发光彩
-

教学技巧 | 巧借问题情境 落实“三会”目标
教学技巧 | 巧借问题情境 落实“三会”目标
-

试题研究 | 光学性质剖析,实例探究思考
试题研究 | 光学性质剖析,实例探究思考
-

试题研究 | 关于椭圆中的蝴蝶模型问题的探究与思考
试题研究 | 关于椭圆中的蝴蝶模型问题的探究与思考
-

试题研究 | 用母函数求解排列问题
试题研究 | 用母函数求解排列问题
-

试题研究 | 多元不等式最值(范围)问题九大处理策略
试题研究 | 多元不等式最值(范围)问题九大处理策略
-

试题研究 | 动态移换问题教学法探究圆与椭圆关联的一类最值问题
试题研究 | 动态移换问题教学法探究圆与椭圆关联的一类最值问题
-

试题研究 | 关于圆锥曲线中的斜率取值问题的探究
试题研究 | 关于圆锥曲线中的斜率取值问题的探究















 登录
登录