目录
快速导航-

数学教育 | RMI原则的理论探析与教学应用思考
数学教育 | RMI原则的理论探析与教学应用思考
-

数学教育 | 高一初期数学教学现状和建议
数学教育 | 高一初期数学教学现状和建议
-

教材研究 | 在教材比较中深度理解数学
教材研究 | 在教材比较中深度理解数学
-
教学研究 | 课程思政视域下高中数学大单元教学的实践与探索
教学研究 | 课程思政视域下高中数学大单元教学的实践与探索
-

教学研究 | 高中数学高效课堂建构中例习题指向深度学习的实践研究
教学研究 | 高中数学高效课堂建构中例习题指向深度学习的实践研究
-

教学研究 | 凝炼核心问题聚焦“四能”培养
教学研究 | 凝炼核心问题聚焦“四能”培养
-
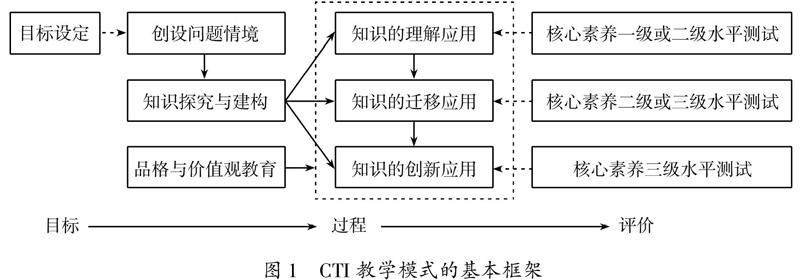
教学研究 | 基于CTI模式的问题链教学设计探索
教学研究 | 基于CTI模式的问题链教学设计探索
-

教学研究 | 基于核心素养培养 合理选择教学内容
教学研究 | 基于核心素养培养 合理选择教学内容
-

教师发展 | 打破思维定势减少解题废招
教师发展 | 打破思维定势减少解题废招
-
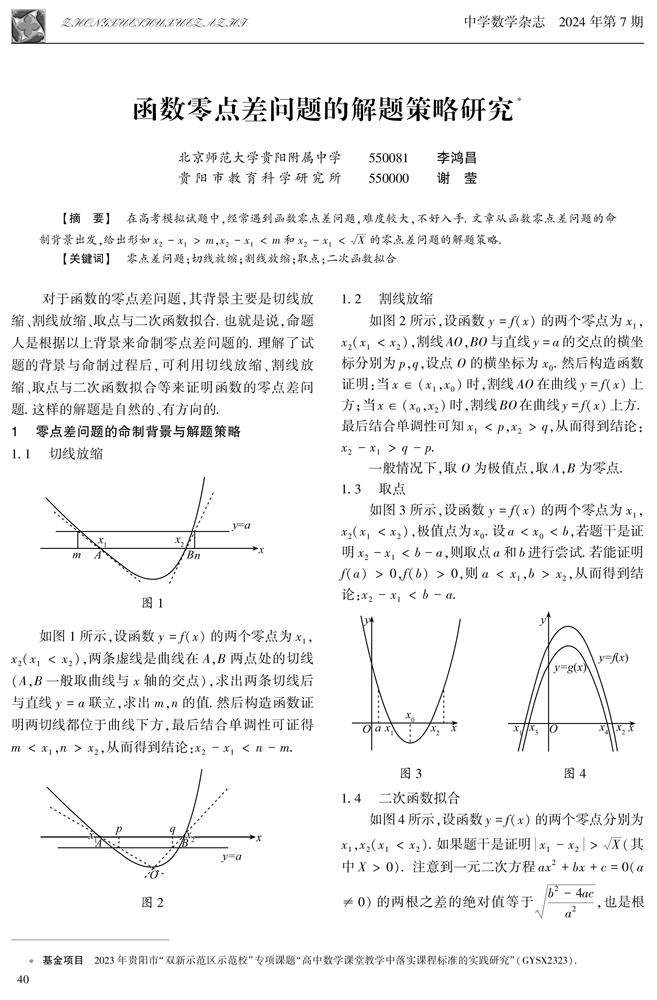
思路与方法 | 函数零点差问题的解题策略研究
思路与方法 | 函数零点差问题的解题策略研究
-

思路与方法 | 九省联考中一道解析几何试题的解法研究
思路与方法 | 九省联考中一道解析几何试题的解法研究
-

高考试题研究 | 2024年高考数学全国Ⅰ卷第18题的多解与思考
高考试题研究 | 2024年高考数学全国Ⅰ卷第18题的多解与思考
-

高考试题研究 | 2024年高考数学新课标Ⅱ卷第19题赏析
高考试题研究 | 2024年高考数学新课标Ⅱ卷第19题赏析
-

高考试题研究 | 2024年高考数学全国Ⅰ卷解析几何题解法研究与复习启示
高考试题研究 | 2024年高考数学全国Ⅰ卷解析几何题解法研究与复习启示
-

高考试题研究 | “立德树人、服务选才、引导教学”是2024年高考数学北京卷的鲜明特色
高考试题研究 | “立德树人、服务选才、引导教学”是2024年高考数学北京卷的鲜明特色










 登录
登录