目录
快速导航-
数学教育 | 数学教育最重要的一些理念
数学教育 | 数学教育最重要的一些理念
-

教材研究 | 注重教材与原创:高中数学模拟试题命制趋向
教材研究 | 注重教材与原创:高中数学模拟试题命制趋向
-

教学研究 | “三会”素养目标下的高中数学新定义问题教学探究
教学研究 | “三会”素养目标下的高中数学新定义问题教学探究
-

教学研究 | “五有四化”主题式教学理念下的“余弦定理”作业设计
教学研究 | “五有四化”主题式教学理念下的“余弦定理”作业设计
-

教学研究 | 巧用数学实验研究高中生的作业设置
教学研究 | 巧用数学实验研究高中生的作业设置
-
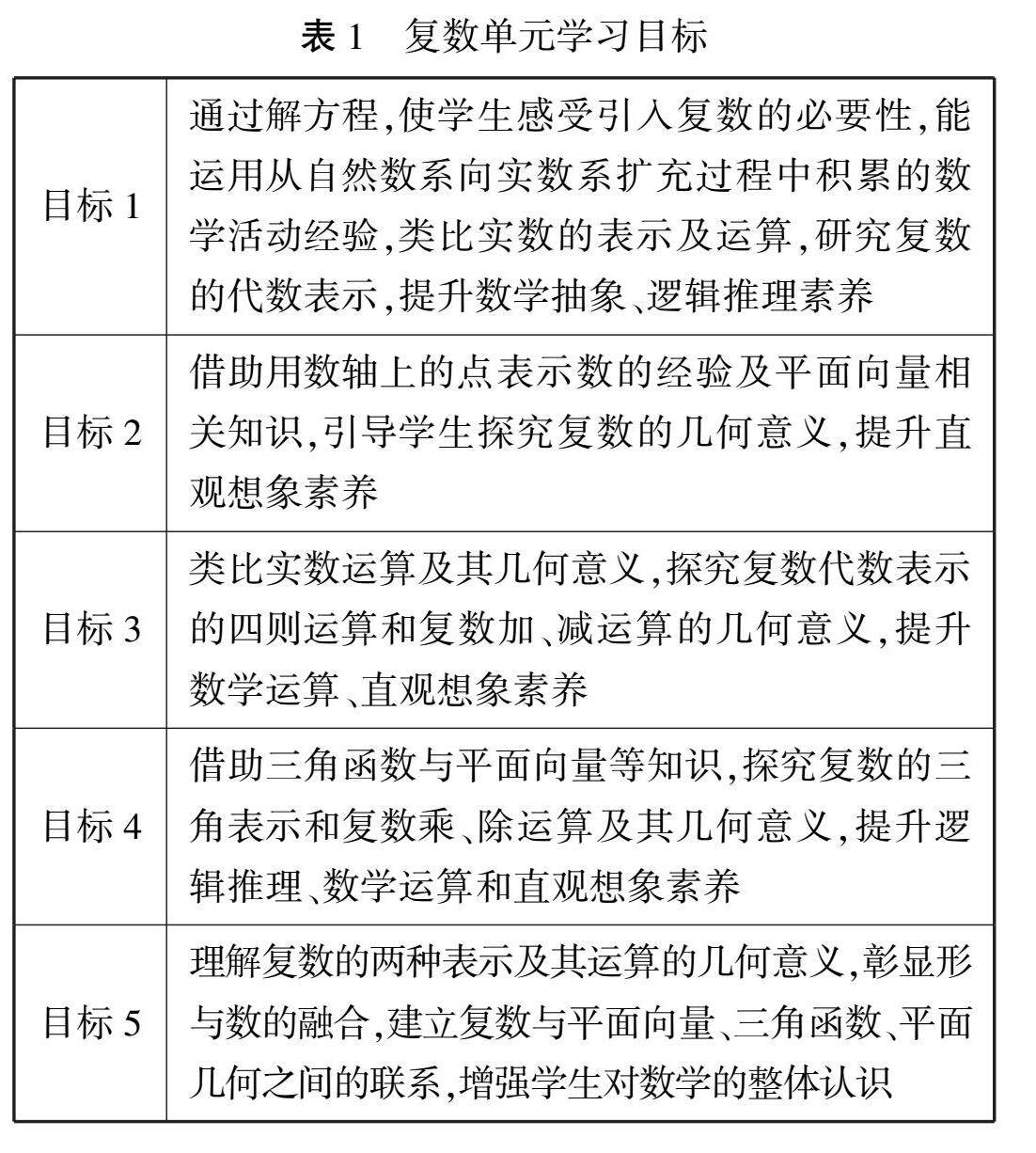
教学研究 | 教学评一致性视角下高中数学单元教学设计研究
教学研究 | 教学评一致性视角下高中数学单元教学设计研究
-

教师发展 | 中学数学教研论文写作的实践与思考
教师发展 | 中学数学教研论文写作的实践与思考
-
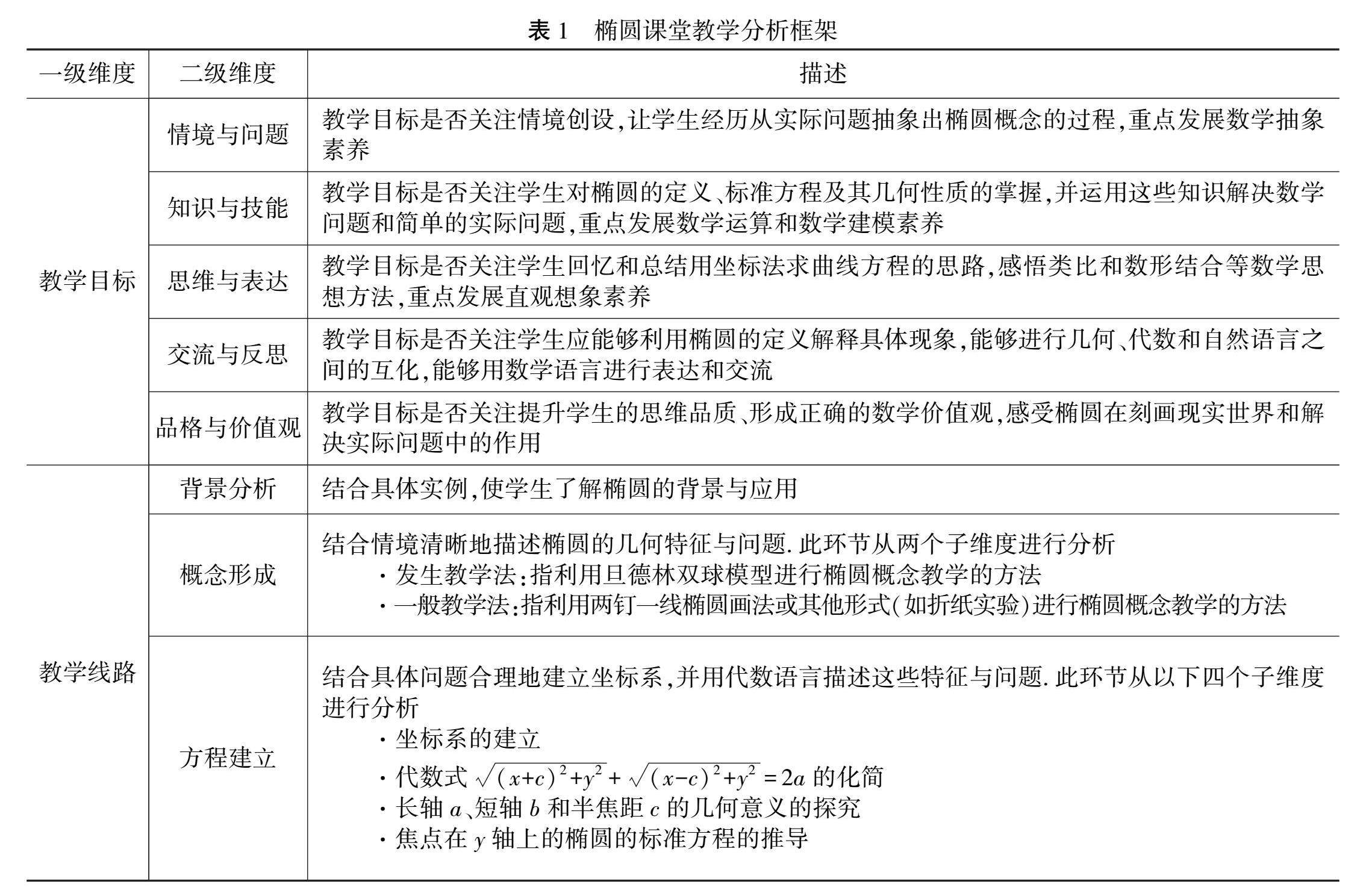
教师发展 | 基于课堂视频的青年教师椭圆课堂教学特征研究
教师发展 | 基于课堂视频的青年教师椭圆课堂教学特征研究
-

学生培养 | 数学自我调节学习对高中生学业成绩的影响研究
学生培养 | 数学自我调节学习对高中生学业成绩的影响研究
-

思路与方法 | 解析几何求范围问题中的“变量”选取技巧
思路与方法 | 解析几何求范围问题中的“变量”选取技巧
-

思路与方法 | 知识梳理建构彼此联系 思维导图呈现命题规律
思路与方法 | 知识梳理建构彼此联系 思维导图呈现命题规律
-

思路与方法 | 例谈如何判断二面角的平面角是锐角还是钝角
思路与方法 | 例谈如何判断二面角的平面角是锐角还是钝角
-

思路与方法 | 一类二次曲线中三角形面积最值问题的探究
思路与方法 | 一类二次曲线中三角形面积最值问题的探究
-
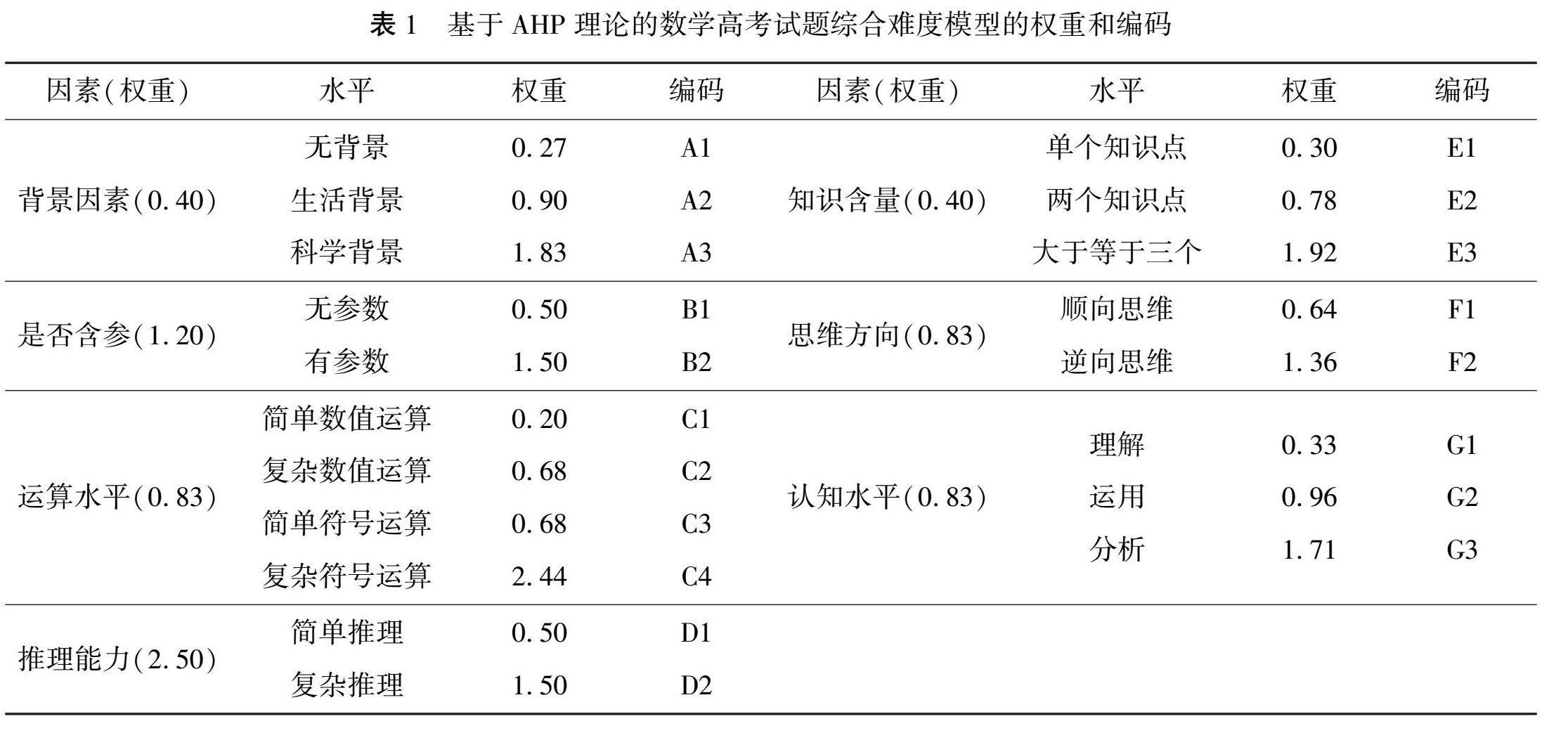
高考复习指导 | 2024年新高考数学综合难度分析及试卷评析
高考复习指导 | 2024年新高考数学综合难度分析及试卷评析
-

高考复习指导 | 对2024年高考数学上海卷第21题的解析与思考
高考复习指导 | 对2024年高考数学上海卷第21题的解析与思考
-

高考复习指导 | 回归几何本源 探究曲线性质
高考复习指导 | 回归几何本源 探究曲线性质










 登录
登录