目录
快速导航-
数学教育 | 《九章算术》中率思想的探索及其教学启示
数学教育 | 《九章算术》中率思想的探索及其教学启示
-
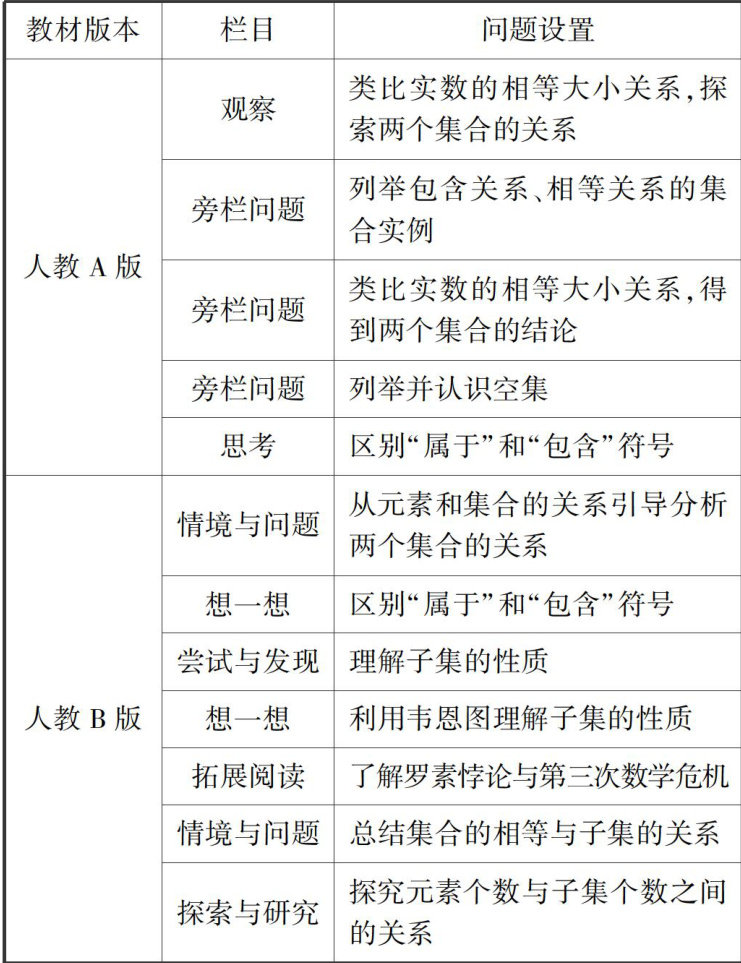
教材研究 | “集合的基本关系”的教材比较分析
教材研究 | “集合的基本关系”的教材比较分析
-
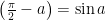
教材研究 | 高中数学新教材引言的变化及教学启示
教材研究 | 高中数学新教材引言的变化及教学启示
-
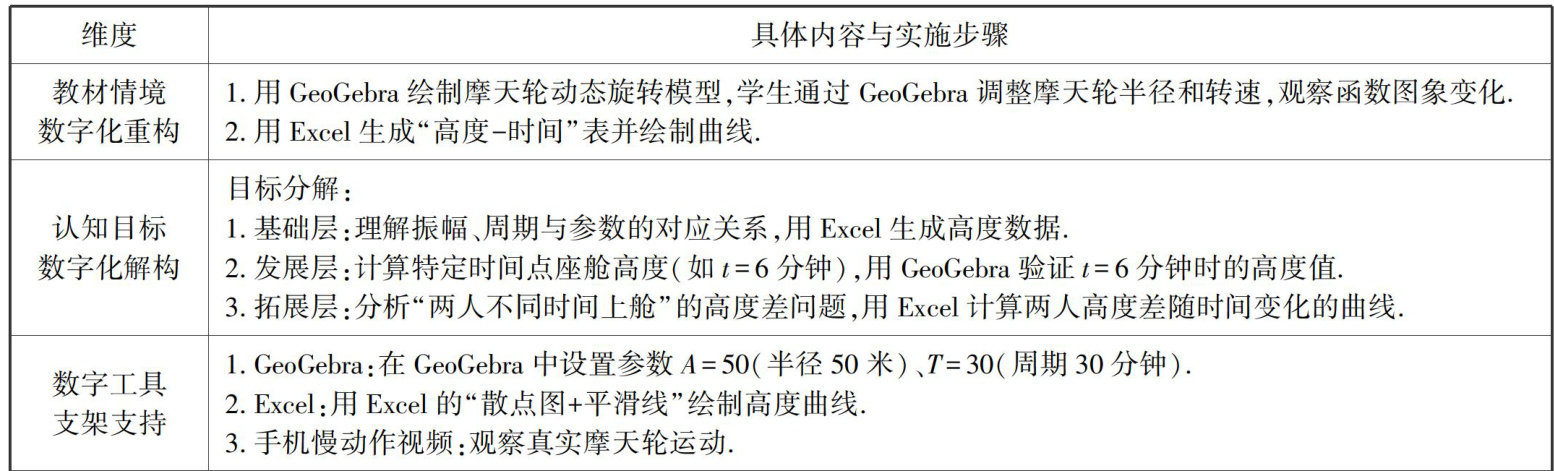
教学研究 | 深度学习导向的高中数学数字化学习资源设计策略
教学研究 | 深度学习导向的高中数学数字化学习资源设计策略
-
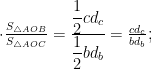
教学研究 | “算两次”原理促进高中数学深度学习探究
教学研究 | “算两次”原理促进高中数学深度学习探究
-

教学研究 | AI赋能高中数学教学变革实践探索
教学研究 | AI赋能高中数学教学变革实践探索
-
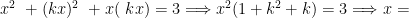
教学研究 | 发散思维培养的内涵、途径及策略
教学研究 | 发散思维培养的内涵、途径及策略
-
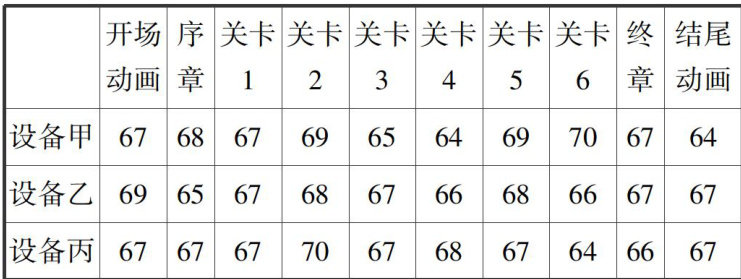
教学研究 | 有关“教学素材”方面的若干思考
教学研究 | 有关“教学素材”方面的若干思考
-
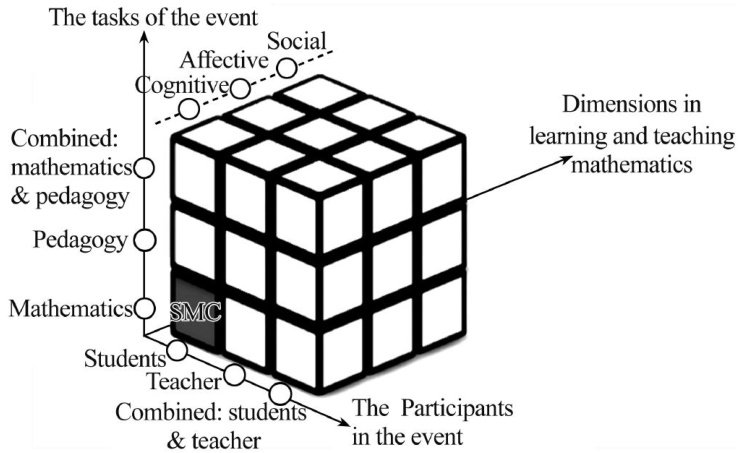
教师发展 | 教学关键事件:促进教师育人智慧的生成
教师发展 | 教学关键事件:促进教师育人智慧的生成
-
教师发展 | 数学人、教育工作者之光
教师发展 | 数学人、教育工作者之光
-
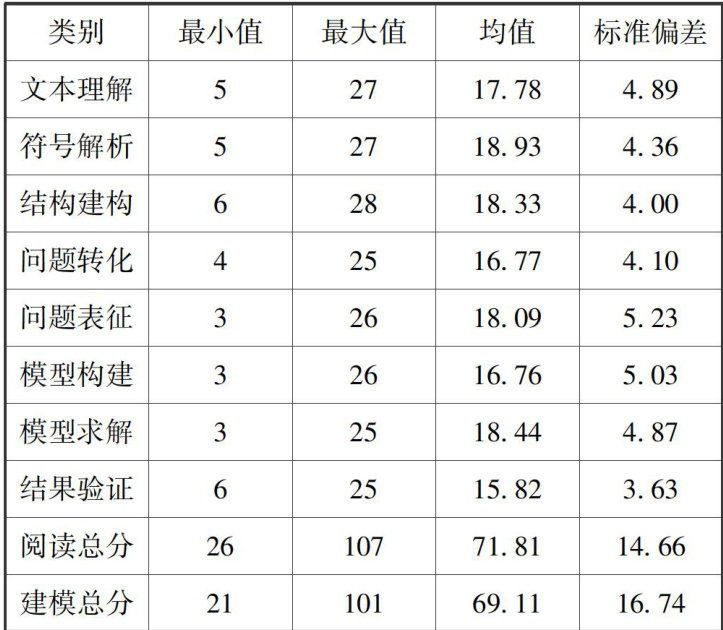
学生培养 | 高中学生数学阅读能力对建模能力的影响研究
学生培养 | 高中学生数学阅读能力对建模能力的影响研究
-
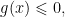
思路与方法 | 基于共零点原理的函数乘积型不等式恒成立问题的系统解法
思路与方法 | 基于共零点原理的函数乘积型不等式恒成立问题的系统解法
-
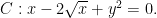
思路与方法 | 分析问题特征 探寻解题方法
思路与方法 | 分析问题特征 探寻解题方法
-
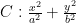
高考试题研究 | 立足数学思维教学 提升数学运算素养
高考试题研究 | 立足数学思维教学 提升数学运算素养
-
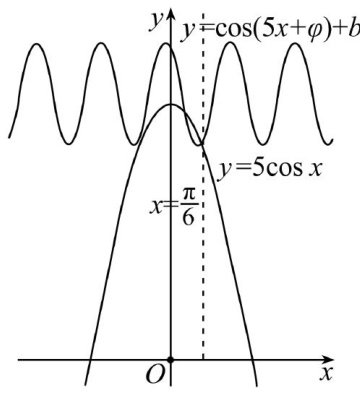
高考试题研究 | 聚焦图形语言转化 构建任意存在直观
高考试题研究 | 聚焦图形语言转化 构建任意存在直观










 登录
登录