目录
快速导航-
数学教育 | 例谈新时代数学命题落实立德树人根本任务的若干视角
数学教育 | 例谈新时代数学命题落实立德树人根本任务的若干视角
-
数学教育 | 以美促成问题求解 因美达成数学素养
数学教育 | 以美促成问题求解 因美达成数学素养
-
教学研究 | 深度学习助力新教师打造优质课堂
教学研究 | 深度学习助力新教师打造优质课堂
1 以深度学习的视角研究课堂教学 深度学习是当下先进的教学思想与方法，近年来受到专家和学者持续关注．在中国知网上搜索，仅关于深度学习的基础教育类数学论文就有数百篇．纵观基于深度学习研究课堂教学的文章，主要侧重于课堂上如何以深度学习提升教学效果，如文献[1～3]．或是基于总体问题的分析，强调深度学习对教师专业发展的意义并提出建议，如文献[4～6]．而结合具体的课堂教学案例进行专业水平提升策略研究的
-
教学研究 | 高中数学课堂“折”资源的有效导引的实践研究
教学研究 | 高中数学课堂“折”资源的有效导引的实践研究
1 课题的提出 高中数学课堂教学是在合作情景下进行的一种教学形式，是高中数学教学最常用的模式．教师通常以活动为载体，营造一个开放的、尊重的、灵活的安全环境，让学生在合作中观察、探讨、分析、发现、归纳．然而课堂教学中存在很多不确定性，如教师的引导调控、活动环节设置、学生的投入程度、周边环境的氛围等都会影响教学效果． 随着教学活动的开展，教师应当在尊重学生的基础上，针对课堂上随机出现或者不可预料的
-
教学研究 | 基于一题一课 探析知识生长
教学研究 | 基于一题一课 探析知识生长
-
教学研究 | 核心素养导向的高中数学新教材教学若干思考
教学研究 | 核心素养导向的高中数学新教材教学若干思考
-
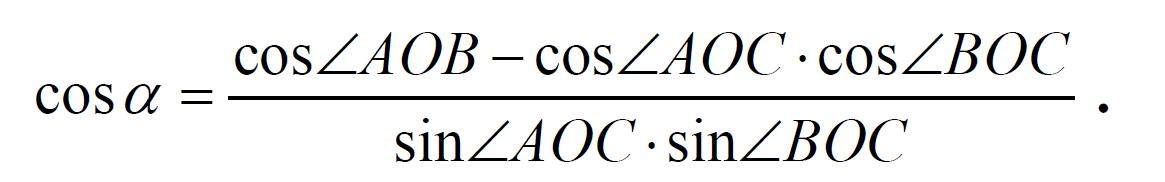
数学探究 | 高中立体几何二面角的解法探究
数学探究 | 高中立体几何二面角的解法探究
-
数学探究 | 再探三直线斜率之商为定值
数学探究 | 再探三直线斜率之商为定值
登录